Statistical Inference
There is a completely general method of accounting for chance which forms the basis of modern statistical reasoning. Inference is the process of combining existing knowledge to get new conclusions, something we do every day. Statistical inference adds the element of uncertainty, where both our information and our conclusions have an element of chance.
The propositional logic of the Greeks gave us a template for reasoning when every variable is exactly true or false: “If it rains, the grass will get wet. The grass is not wet. Therefore it did not rain today.” The theory of statistical inference extends this to uncertain information and uncertain answers: “There was a 40 percent chance of rain today. It’s hard to say from just looking out my window, but I’m 70 percent sure the grass is dry. What’s the probability that it rained today?”
The most comprehensive modern theory is usually called Bayesian statistics after its roots in Reverend Bayes’s theorem of 1763. But the practical method was only fully developed in the twentieth century with the advent of modern computing. If you’ve never seen this sort of thing before, it’s unlikely that this little introduction will prepare you to do your own analyses. We can’t cover all of Bayesian statistics in a few pages, and anyway there are books on that.xvi Instead I’m going to walk through a specific Bayesian method, a general way to answer multiple-choice questions when the answer is obscured by randomness. My purpose is to show the basic logic of the process, and to show that this logic is commonsensical and understandable. Don’t let statistics be mysterious to you!
Bayesian statistics works by asking: What hypothetical world is most likely to produce the data we have? And how much more likely is it to do so than the alternatives? The possible “worlds” are captured by statistical models, little simulations of hypothetical realities that produce fake data. Then we compare the fake data to the real data to decide which model most closely matches reality.
With the multiple-choice method in this chapter you can answer questions like “how likely is it that the average number of assaults per quarter really decreased after the earlier closing time?” Or “if this poll has Nunez leading Jones by 3 percent but it has a 2 percent margin of error, what are the chances that Nunez is actually the one ahead?” Or “could the twentieth century’s upward global temperature trend be just a fluke, historically speaking?”
We’ll work through a small example that has the same shape as our assaults versus closing time policy question. Suppose there is a dangerous intersection in your city. Not long ago there were nine accidents in one year! But that was before the city installed a traffic light. Since the stoplight was installed there have been many fewer accidents.

Accident data surely involves many seemingly random circumstances. Maybe the weather was bad. Maybe a heartbroken driver was distracted by a song that reminded them of their ex. A butterfly flaps its wings, etc.xvii Nonetheless, it is indisputably true that there were fewer accidents after the stoplight was installed.
But did the stoplight actually reduce accidents? We might suspect that a proper stoplight will cut accidents in half, but we have to regard this possibility as a guess, so we say it’s a hypothesis until we find some way to prove it. We’re going to compare the following hypotheses:
The stoplight was effective in reducing accidents by half.
The stoplight did nothing, meaning that the observed decline in accidents is just luck.
The next thing we need is a statistical model for each hypothesis. A model is a toy version of the world that we use for reasoning. It incorporates all our background knowledge and assumptions, encapsulating whatever we might already know about our problem. Silver used a simple model, based on the odds of any given person dying on any given day, to estimate the odds of three people dying on the same day at any of 5,000 clinics. Peirce created a model based on the stroke positions of 42 signatures that were known to be genuine. A model is by definition a fake. It’s not nearly as sophisticated as reality. But it can be useful if it represents reality in the right way. Creating a model is a sort of quantification step, where we encode our beliefs about the world into mathematical language.
For our purposes a model is a way to generate fake data, imagined histories of the world that never occurred. We’ll need two assumptions to build a simple model of our intersection. We’ll assume that the same number of cars pass each day, and we’ll pick the number based on the historical data we have. We’ll further assume that there is some percentage chance of each car getting into an accident as it does, and again we’ll use historical data, pre-stoplight, to guess at the proper percentage.
With these two numbers in hand you can imagine writing a small piece of code to simulate the intersection. As each simulated car goes into the simulated intersection we can flip a simulated coin to determine whether to count an accident. We calibrate the “coin” so the cars crash at the proper percentage. This is a reasonable model if we are willing to assume that car accidents are independent: there might have been an accident at this intersection a year or an hour ago but that doesn’t change the odds that you are about to have an accident.xviii
By setting up the simulation to produce the same average accident rate as we saw pre-stoplight, we’ve built a model of the intersection without the stoplight that we hope matches the real world. We can use this model to get a feel for the range of scenarios that chance can produce by running the simulation many times, like this:
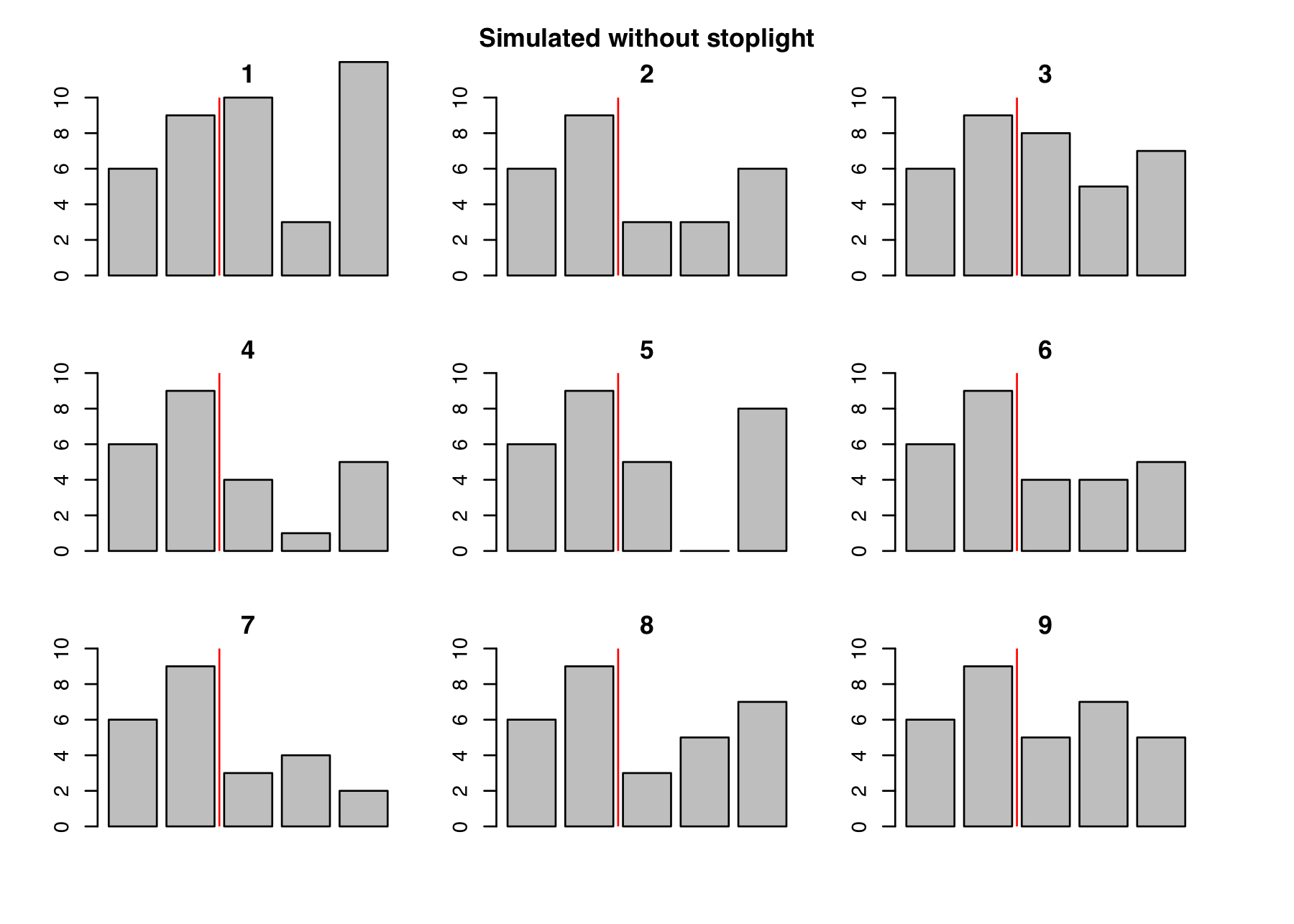
The first two years in each of these charts are just the original data, pre-stoplight. The last three years have been generated by simulation. In some of these alternate histories the number of accidents decreased relative to the pre-stoplight years, and in others the pattern was increasing or mixed, all purely by chance. In order to compare models, we first need to pick a more precise definition of “decline.” So let’s say that the accidents “declined” if all the post-stoplight years show fewer accidents than any of the pre-stoplight years—just like the real data from the actual intersection. This is a somewhat arbitrary criterion, but your choice determines exactly which hypotheses you are testing. Just as our simulation expresses the world in code, our test criterion expresses the hypotheses mathematically. By our chosen test, scenarios 4, 6, and 7 show a decrease in the accident rate. We are counting the branches of a tree of possibilities once more.
They key number is how often we see the effect without the alleged cause, just like the vaccine deaths and Howland will case. None of these alternate histories include a stoplight, yet we see a decline after the second year in 3/9 cases, which is a probability of 0.33. This makes the “chance decline” theory pretty plausible. A probability of 0.33 is a 33 percent chance, which may not seem “high” compared to something that happens 90 percent of the time, but if you’re rolling dice you’re going to see anything that happens 33 percent of the time an awful lot.
This doesn’t make the “chance decline” hypothesis true. Or false. It especially does not mean that the chance decline theory has a 33 percent chance of being true. We assumed that “chance decline” was true when we constructed the simulation. In the language of conditional probability, we have computed p(data | hypothesis) which is read “the probability of the data given the hypothesis.” What we really want to know is p(hypothesis | data), the probability that the hypothesis is true given the data. The distinction is kind of brain bending, I admit, but the key is to keep track of which way the deduction goes.
As we saw in the last section, the more likely it is that your data was produced by chance, the less likely it was produced by something else. But to finish our analysis we need a comparison. We haven’t yet said anything at all about the evidence for the “stoplight worked” theory.
First we need a model of a working stoplight. If we believe that a working stoplight should cut the number of accidents in half in an intersection like this, then we can change our simulation to produce 50 percent fewer accidents. This is an arbitrary number; a more sohisticated analysis would test and compare many possible numerical values for the reduction in accidents. Here’s the result of simulating a 50 percent effective stoplight many times:
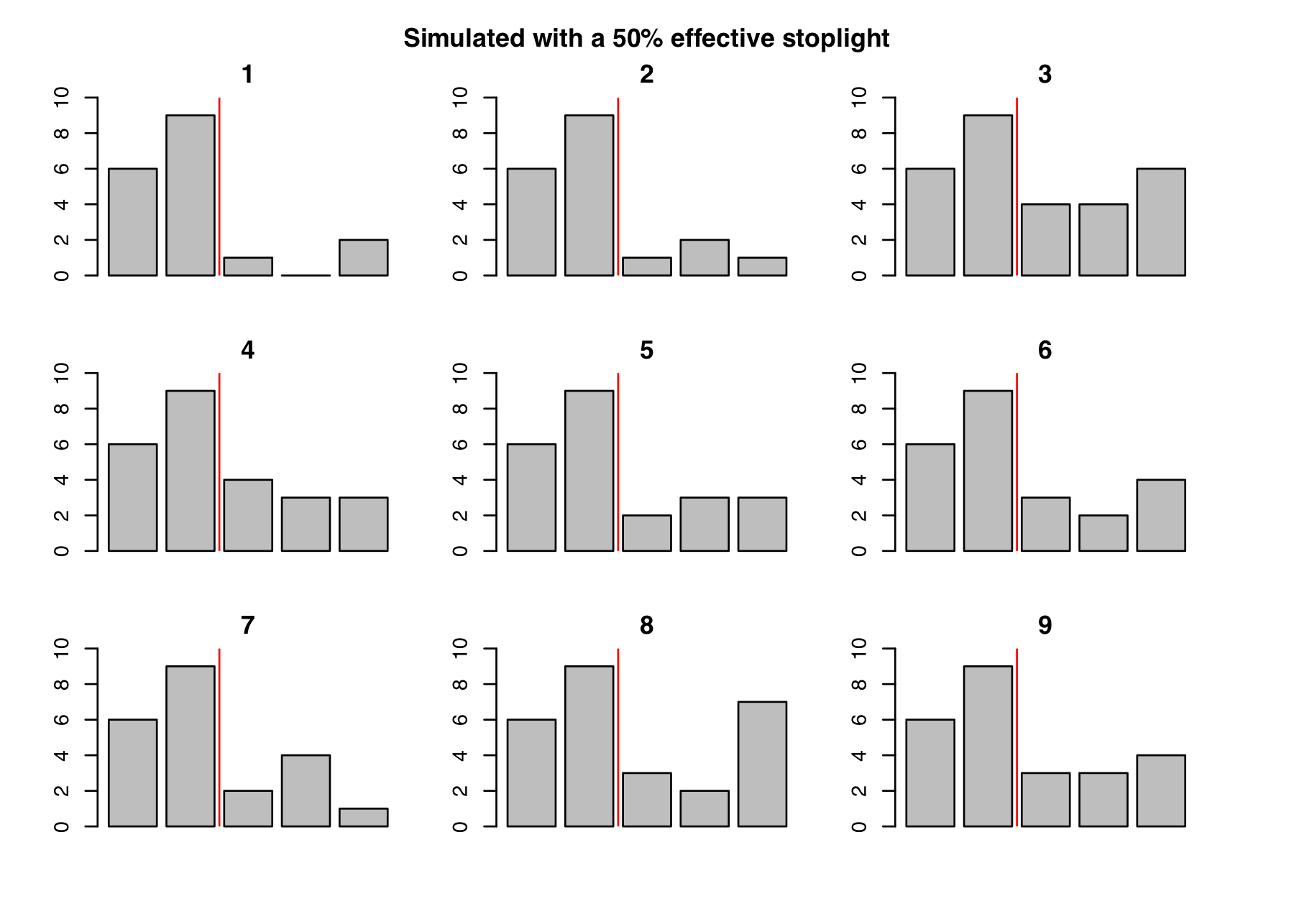
Again, each of these charts is a simulated alternate history. The first two years of data on each chart is our real data and the last three years are synthetic. This time the simulation produces half as many accidents on average for the last three years, because that’s how effective we believe the stoplight should be. By our criterion that every post-stoplight year should be lower than every pre-stoplight year, there’s a reduction in accidents in simulations 1, 2, 4, 5, 6, 7, and 9. This is 7 out of 9 scenarios declining, or a 7 / 9 = 0.78 probability that we’d see a decline like the one we actually saw, if the stoplight reduced the overall number of accidents by half.
This is good evidence for the “stoplight cut accidents in half” hypothesis. But the probability of seeing this data by chance is 0.33, which is also pretty good. This is not a situation like Mrs. Howland’s will where the odds of one hypothesis were miniscule (identical signature by chance) while the odds of the other hypothesis were good (forged signature to get millions of dollars).
Finally we arrive at a numerical comparison of two hypotheses in the light of chance effects. The key figure is the ratio of the probabilities that each model generates data like the data actually observed. This is called the likelihood ratio or Bayes factor, and you can think of it as the odds in favor of one model as compared to another. The key idea of comparing multiple models was fleshed out in the early twentieth century by figures such as R. A. Fisher32 and Harold Jeffreys.33
The probability that “stoplight cut accidents in half” could generate our declining data is 0.78 while the probability that “chance decline” accounts for the data is 0.33, so the Bayes factor is 0.78 / 0.33 = 2.3. This means that the odds of the “stoplight worked” model generating the observed data, when compared to the “chance decline” model, are 2.3 to 1 in favor.
This doesn’t make the “stoplight cut accidents in half” story true. But it definitely seems more likely.
These 2.3 to 1 odds are middling. Converting the odds to a probability, that’s a 2.3 / (2.3+1) = 70 percent chance the stoplight worked. That means if you write a story which says it did work, there’s a 30 percent chance you’re wrong. In other situations you might have a 90 percent or 99 percent or even 99.9 percent chance of guessing correctly. But there can be no fixed scale for evaluating the odds, because it depends on what’s at stake. Would 2.3 to 1 odds be good enough for you to run a story that might look naive later? What if that story convinced the city government to spend millions on stoplights that didn’t work? What if your story convinced the city government not to spend millions on stoplights that did work, and could have saved lives?
Even so, “stoplight worked” is a better story than “chance decline.” A better story than either would be “stoplight probably worked.” Journalists, like most people, tend to be uncomfortable with intermediate probability values. A 0 percent or 100 percent chance is easy to understand. A 50/50 chance is also easy: You know essentially nothing about which alternative is better. it’s harder to know what to do with the 70/30 chance of our 2.3 to 1 odds. But if that’s your best knowledge, it’s what you must say.
In real work we also need to look at more than the data from just one stoplight. We should be talking to other sources, looking at other data sets, collecting all sorts of other information about the problem. Fortunately there is a natural way to incorporate other knowledge in the form of prior odds, which you can think of as the odds that the stoplight worked given all other evidence except your data. This comes out in the mathematical derivation of the method, which says we need to multiply our Bayes factor of 2.3 to 1 by the prior odds to get a final estimate.
Maybe stoplight effectiveness data from other cities shows that stoplights usually do reduce accidents but seem to fail about a fifth of the time, so you pick your prior odds at 4 to 1. Multiplying by your 2.3 to 1 strengthens your final odds to 9 to 1. The logic here is: stoplights in other cities seem to work, and this one seems to work too, so the totality of evidence is stronger than the data from just this one stoplight.
Or maybe you have talked to an expert who tells you that stoplights usually only work in large and complex highway intersections, not the quiet little residential intersection we’re looking at, so you pick prior odds of 1 to 5, which could also be written 0.2 to 1. In this case even our very plausible data can’t overwhelm this strong negative evidence, and the final odds are 2.3 x 0.2 = 0.46 to 1, meaning that it’s more than twice as likely that the stoplight didn’t work. The logic here is: most stoplights at this kind of intersection don’t work, and this undermines the evidence from this one stoplight, which leads us to believe that the observed decline is more likely than not just due to chance.
Multiplying by the prior is mathematically sound, yet it’s often unclear how to put probabilities on available evidence. If the mayor of Detroit tells you she swears by stoplights in her city, what does this say about the odds of stoplights working versus not working as a numeric value? There is no escape from judgment. But even very rough estimates may be usefully combined this way. If nothing else, the existence of the prior in statistical formulas helpfully reminds us to consult all other sources!
There is a lot more to say about this method of comparing the likelihood that different models generated your data. The method here only applies to multiple-choice questions, whereas real work often estimates a parameter: how much did the stoplight reduce accidents? And we’ve barely touched on modeling, especially the troubling possibility that all of your models are such poor representations of reality that the calculations are meaningless.xix But the fundamental logic of comparing how often different possibilities would produce your observed data carries through to the most complex analyses. I hope this example gives the flavor of how a single unifying framework has been used to solve problems in medicine, cryptography, ballistics, insurance, and just about every other human activity.34 Bayesian statistics is something remarkable, and I find its wide success incredible, unlikely, and almost shockingly too good to be true. You can always start from the general framework and work your way toward the details of your problem. This is sometimes more work, but it is the antidote to staring at equations and wondering if they apply.